在ACT数学中时常会考到二次函数图像的平移，小编为大家系统的整理了几种情况，并结合ACT典型例题为大家讲解，一起来学习一下吧。

　　例：The graph of y=x² is shown in the standard (x,y) coordinate plane below.For which of the following equations is the graph of the parabola shifted 3 units to the right and 2 units down?

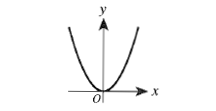
　　F.y=(x+3)²+2 G.y=(x+3)²-2 H.(x-2)²+3 J.(x-3)²+2 K.(x-3)²-2

　　解析：本题考查的是二次函数图像的平移知识，我们先回忆一下相关知识再做题。

　　二次函数解析式的几种表达式：

　　(1)一般式：y=a²+bx+c (a，b，c为常数，a≠0)。

　　(2)顶点式：y=a(x-h)²+k(a，h，k为常数，a≠0)。

　　(3)两根式：y=a(x-x1)(x-x2)，其中x1，x2是抛物线与x轴的交点的横坐标，即一元二次方程a²+bx+c=0的两个根，a≠0。

　　在考查图像的平移及对称轴知识时，我们通常会把二次函数写成顶点式，根据对称轴及顶点的变化在原方程上改写新的方程。

　　平移规律(以y=x²为例)：

　　(1)沿x轴向左移m个单位，则对称轴向左移m个单位，新的二次函数方程为

　　y=(x+m)²，向右移同理;

　　(2)沿y轴向上移n个单位，则对称轴不变，新的二次函数方程为y=x²+n，向下移同理。

　　所以例题中向右平移三个单位后向下平移2个单位的新的图像方程为y=(x-3)²-2 选择K。

　　根据这两条规律就可以解决在ACT数学考试中关于二次函数图像的平移这类问题，ACT数学中对二次函数的考查大多涉及到图像、周期、极值、单调性几方面内容，磨刀不误砍柴工，大家在平时要注意基础知识的巩固。最后，前程百利祝大家在ACT考试中取得优异的成绩。

您还可能关注：

前程百利托福小班辅导

前程百利外教小班

前程百利一对一辅导课程

百利大师兄，留学考试百事通！随时在线答疑，咨询出国留学、出国考试全方位解答，更有免费托福模考评分+讲解，免费微课！微信号：bailiedu2015，快快添加吧！

• 免费模考
• 在线咨询